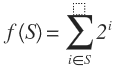今天看到一个问题：

Given an array of integers, every element appears twice except for one. Find that single one.

本能的想法是建立一个数组a[]，每个元素初始化为0，如果数字x出现，就让a[x]+=1。但是很多时候内存消耗太大了，因为x可以很大。

另一个想法是把所有数字保存到数组a中，然后排序，最后线性扫描一遍找出答案。比之前的方法更可行，但是我发现还有更好的方法。

这个方法需要运用位运算的知识。思路就是每位bit出现2次就清零，所以可以不断异或运算得出最终结果。

int singleNumber(int A[], int n) {
    int ans = 0;
    for (int i = 0; i < n; i++) ans ^= A[i];
    return ans;
}

类似的问题还有很多，比如下面这个，稍微比之前的更难一些：

Given an array with N integers where all elements appear three times except for one. Find out the one which appears only once.N($1\le N\le { 10 }^{ 5 }$),All elements are ranged in $\left[ 0,{ 2 }^{ 63 }-1 \right]$ .

对于每个二进制位，如果出现次数是3的倍数，就将其清零，剩下的就是最终的数。

用ones记录到当前计算的变量为止，二进制1出现“1次”的数位。用twos记录到当前计算的变量为止，二进制1出现“2次”的数位。当ones和twos中的某一位同时为1时表示二进制1出现3次，此时需要清零。最终ones记录的是最终结果。

int singleNumber(int A[], int n) {
    int ones = 0, twos = 0, xthrees = 0;
    for(int i = 0; i < n; ++i) {
        twos |= (ones & A[i]);
        ones ^= A[i];
        xthrees = ~(ones & twos);
        ones &= xthrees;
        twos &= xthrees;
    }

    return ones;
}

在布莱叶盲文中，字符全由六个点绘制。这六个点，凸起或者不凸起一共有64种状态，也就是可以表示64种信息。

下面是小写字母表：

w那么特殊是因为在传统的法语中不会用到它。

经过仔细的检查，你会发现，从我们列举的那个三排布莱叶盲文的例子（小写字母表）中，可以总结出一个规律。第一排（字母a到j）只用到了点码单元中最上面的四个点–第1、2、4和5点。第二排在复用了第一排的编码的基础上，把第3点改为凸点。第三排也沿用了同样的规律，只是将第3和6点改为凸点。

具体使用的时候，每个单词之间和我们的习惯一样，用空格隔开。

但是64个变量中我们到现在只用了26个，这是极大的浪费。为了使用方便，布莱叶盲文定义了一些常用的字符集合。

其中，数字的表示如下。

加上前缀之后，表示后面的点阵表示数字。

最后，六号凸点表示后面的一个字母大写。

在程序中表示集合的方法有很多种，当元素比较少时，用二进制码来表示比较方便。集合{0,1,…n-1}的子集S可以用如下方式编码成整数。

像这样之后，一些集合运算可以对应写成如下方式。

空集	0
只含有第i个元素的集合{i}	1<<i
含有全部n个元素的集合{0,1,...,n-1}	(1<<n)-1
判断第i个元素是否属于集合S	if(S>>i&1)
向集合中加入第i个元素	S|1<<i
从集合S中去除第i个元素S-{i}	S&~(1<<i)
S和T的并集	S|T
S和T的交集	S&T

将集合{0,1,…,n-1}的所有子集枚举出来，可以像这样写

<pre id=’vimCodeElement’style=”font-family: monospace; color: #839496; background-color: #002b36;”> for(int S = 0; S < 1 << n; S++) { //处理子集 } </pre>

枚举集合sup的子集。sup是一个二进制码，可能不是全集，其本身也是某个集合的子集。例如给定01101101这样的集合，要将01100000或者00101101等这样的子集枚举出来。

int sub = sup;
do {
    //处理子集
    sub = (sub - 1) & sup;
} while(sub != sup); //处理完0之后，会有-1&sup=sup

枚举{0,1,…,n-1}的所有容量为k的子集

int comb = (1 << k) - 1;
while (comb < 1 << n) {
    //处理组合
    int x = comb & -comb, y = comb + x;
    comb = ((comb & ~y) / x >> 1) | y;
}

从(1«k)-1开始，求出其后的集合的方法。

1. 求出最低位的1开始的连续的1区间(0101110->0001110)
2. 将这一区间全部变成0，并将区间左侧的那个0变成1(0101110->0110000)
3. 将第一步的区间右移，直到剩下的1的个数减少了1个(0001110->0000011)
4. 将第二步和第三步的结果按位或(0110000|0000011=0110011)

x=comb&-comb 就是最低位的1独立出来后的值。-comb对应(~comb)+1。 y=comb+x 将最低位从1开始，连续的1都置零，区间左侧的那个0变成1。 z=comb&~y 得到最低位从1开始的连续区间。 z/x 将z不断右移，直到最低位为1，只要再向右移一位就是第三步的结果。

例如

comb = 0101110
   x = 0000010
   y = 0110000
   z = 0001110