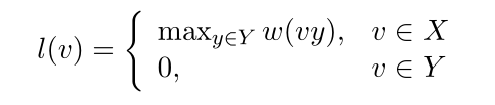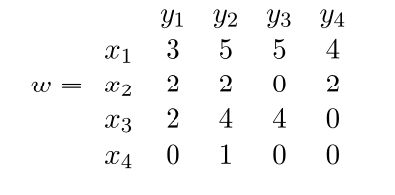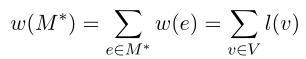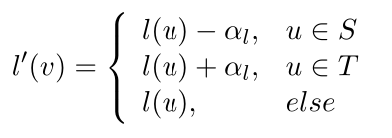最优指派问题
欲安排 n 个人员 $x_1, x_2, \cdots, x_n$ 从事 n 项工作 $y_1, y_2,\cdots, y_n$ ,已知每个人能胜任其中一项或几项工作,各人做不同工作的效率不同. 求一种工作安排,使得每个人分配一项不同于其他人的工作,且使总的工作效率最大.
图论描述
给定赋权二部图 $K_{n,n} = (X, Y) : X = \{x_1, x_2, \cdots, x_n\}, Y = \{y_1, y_2,\cdots, y_n \}$,边$x_iy_j$有权$w_{ij}$(权值为0表示不胜任工作). 求$K_{n,n}$的一个具有最大权的完美匹配.
| 一般地,给定一个赋权二部图G={X,Y}(未必 |
X |
= |
Y |
),可以添加一些定点及一些权值为0的边以转化问题. |
算法理论基础
图 G 的顶点标号是从顶点到正整数集的一个映射,用l(v)表示顶点 v 的标号, w(uv)表示边(u, v)的权. 对于赋权二部图 G = {X, Y},若对每条边 e = xy,均有 $l(x)+l(y)\ge w(xy)$,则称这个标号为 G 的一个可行定点标号。
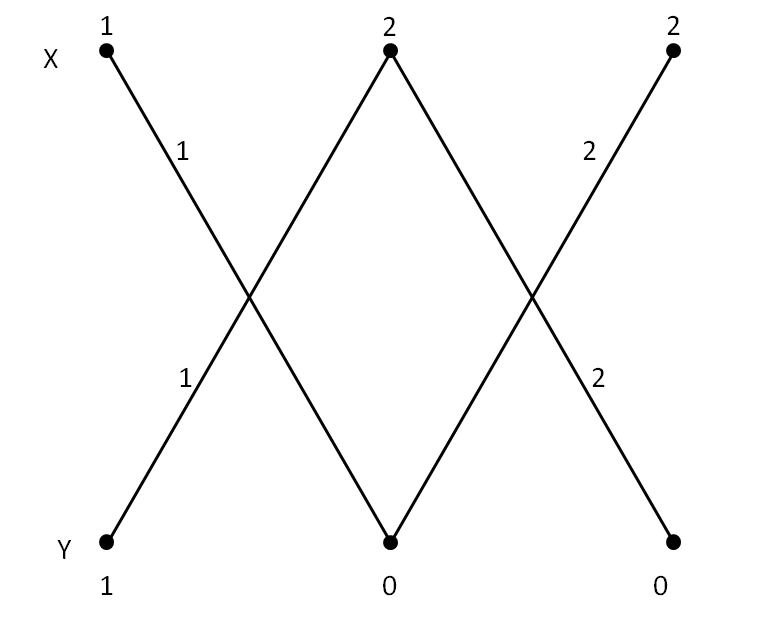
赋权二部图的可行顶点标号总是存在的. 一种平凡的可行顶点标号是:对$\forall v \in V$,
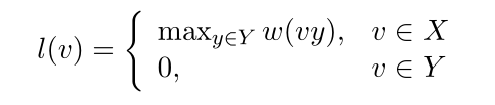
设 G 是一个赋权二部图,l 是 G 的可行顶点标号,边 (u, v) 上的权为 w(uv),令
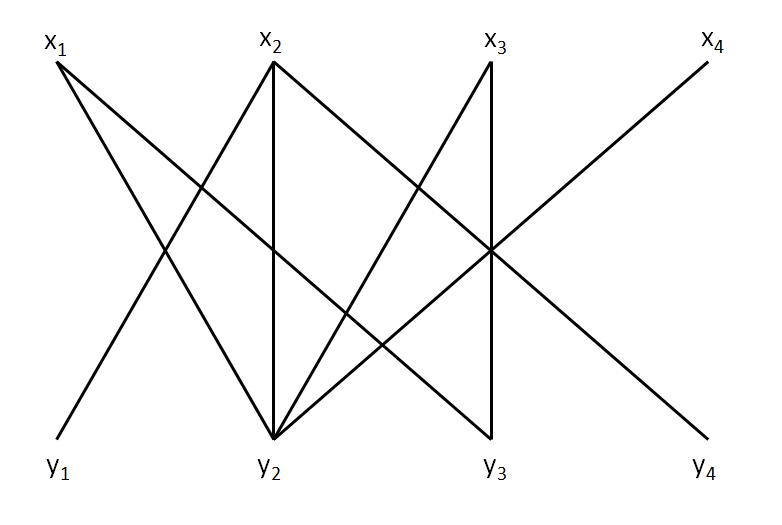
G 中以 $E_l$ 为边集的生成子图称为 G 的 l 相等子图,记为 $G_l$.
下面的例子显示了一个赋权完全二部图 $G=K_{4,4}$的平凡顶点标号,以及这种标号下的相等子图.
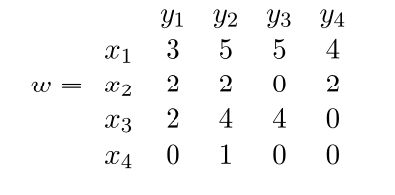

定理
设l是赋权二部图 G 的一个可行顶点标号. 若相等子图$G_l$有完美匹配$M^* $,则$M^* $ 是G的最大权完美匹配.
证明
由于相等子图 $ G_l $ 是G的生成子图,固 $ G_l $ 的完美匹配 $ M^* $ 也是 G 的完美匹配,而且
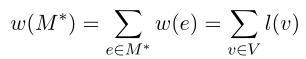
另一方面,对 G 的任何完美匹配 M,有:

可见 $W(M^* )\ge W(M)$ ,即 $M^* $ 是 G 的最大权完美匹配. 证毕.
算法思想
Kuhn和Munkres给出修改标号的方法,使得新的相等子图的最大匹配逐渐扩大,最终的到完美匹配的相等子图.
首先给出赋权二部图 G 的任意一个可行顶点标号(如平凡标号),然后决定相等子图 $ G_l $ ,在 $ G_l $ 中执行匈牙利算法. 若在 $ G_l $中找到完美匹配,则它就是 G 的最大完美匹配. 否则,匈牙利算法终止于 $ S\subset X, T\subset Y $ ,且 $ N_{G_{l}}=T $ 如下图所示.
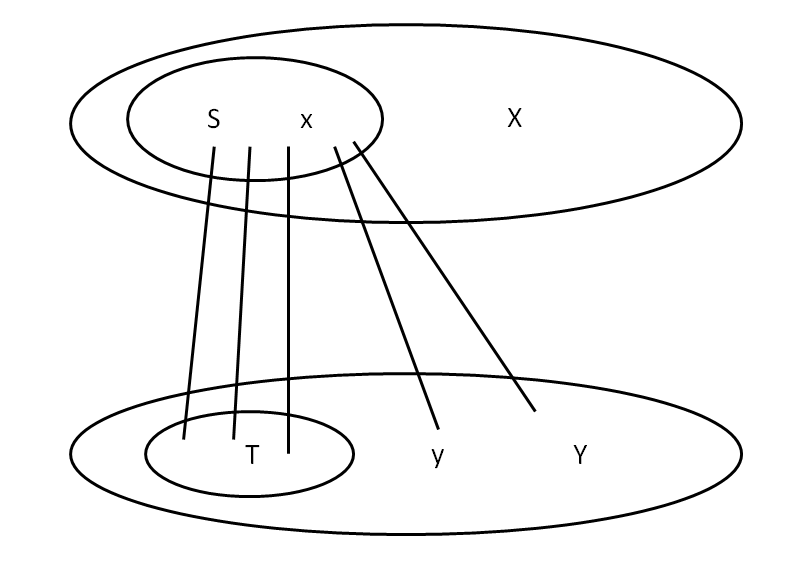
设当前找到的匹配为 M. 令
对每个顶点u,修改其标号如下
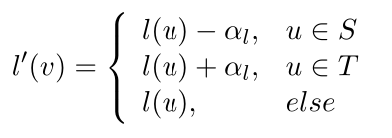
可以检验$l’$仍是 G 的一个可行顶点标号.用 $l’$代替$l$,获得新的相等子图 $G’$.
参考代码
1 /*
2 * w 表示带权图
3 * pop表示图一侧的顶点数
4 *
5 * 返回对大权匹配的权值
6 * son_y 表示匹配方案
7 */
8 const int maxn = 222;
9 const int inf = 1000000000;
10
11 int mymin(int a, int b) {
12 return a > b ? b : a;
13 }
14 int mymax(int a, int b) {
15 return a > b ? a : b;
16 }
17
18 int w[maxn][maxn], x[maxn], y[maxn];
19 int prev_x[maxn], prev_y[maxn], son_y[maxn], slack[maxn], par[maxn];
20 int lx, ly, pop;
21 void adjust(int v) {
22 son_y[v] = prev_y[v];
23 if(prev_x[son_y[v]] != -2)
24 adjust(prev_x[son_y[v]]);
25 }
26 bool find(int v) {
27 int i;
28 for(i = 0; i < pop; i++)
29 if(prev_y[i] == -1) {
30 if(slack[i] > x[v] + y[i] - w[v][i]) {
31 slack[i] = x[v] + y[i] - w[v][i];
32 par[i] = v;
33 }
34 if(x[v] + y[i] == w[v][i]) {
35 prev_y[i] = v;
36 if(son_y[i] == -1) {
37 adjust(i);
38 return true;
39 }
40 if(prev_x[son_y[i]] != -1)
41 continue;
42 prev_x[son_y[i]] = i;
43 if(find(son_y[i]))
44 return true;
45 }
46 }
47 return false;
48 }
49 int km() {
50 int i, j, m;
51 for(i = 0; i < pop; i++) {
52 son_y[i] = -1;
53 y[i] = 0;
54 }
55 for(i = 0; i < pop; i++) {
56 x[i] = 0;
57 for(j = 0; j < pop; j++)
58 x[i] = mymax(x[i], w[i][j]);
59 }
60 bool flag;
61 for(i = 0; i < pop; i++) {
62 for(j = 0; j < pop; j++) {
63 prev_x[j] = prev_y[j] = -1;
64 slack[j] = inf;
65 }
66 prev_x[i] = -2;
67 if(find(i)) continue;
68 flag = false;
69 while(!flag) {
70 m = inf;
71 for(j = 0; j < pop; j++)
72 if(prev_y[j] == -1)
73 m = mymin(m, slack[j]);
74 for(j = 0; j < pop; j++) {
75 if(prev_x[j] != -1)
76 x[j] -= m;
77 if(prev_y[j] != -1)
78 y[j] += m;
79 else
80 slack[j] -= m;
81 }
82 for(j = 0; j < pop; j++)
83 if(prev_y[j] == -1 && !slack[j]) {
84 prev_y[j] = par[j];
85 if(son_y[j] == -1) {
86 adjust(j);
87 flag = true;
88 break;
89 }
90 prev_x[son_y[j]] = j;
91 if(find(son_y[j])) {
92 flag = true;
93 break;
94 }
95 }
96 }
97 }
98 int ans = 0;
99 for(int i = 0; i < pop; i++)
100 ans += w[son_y[i]][i];
101 return ans;
102 }