集合的整数表示

在程序中表示集合的方法有很多种，当元素比较少时，用二进制码来表示比较方便。集合{0,1,…n-1}的子集S可以用如下方式编码成整数。

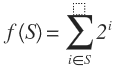
像这样之后，一些集合运算可以对应写成如下方式。

空集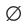	0
只含有第i个元素的集合{i}	1<<i
含有全部n个元素的集合{0,1,...,n-1}	(1<<n)-1
判断第i个元素是否属于集合S	if(S>>i&1)
向集合中加入第i个元素	S|1<<i
从集合S中去除第i个元素S-{i}	S&~(1<<i)
S和T的并集	S|T
S和T的交集	S&T

将集合{0,1,…,n-1}的所有子集枚举出来，可以像这样写

<pre id=’vimCodeElement’style=”font-family: monospace; color: #839496; background-color: #002b36;”> for(int S = 0; S < 1 << n; S++) { //处理子集 } </pre>

枚举集合sup的子集。sup是一个二进制码，可能不是全集，其本身也是某个集合的子集。例如给定01101101这样的集合，要将01100000或者00101101等这样的子集枚举出来。

int sub = sup;
do {
    //处理子集
    sub = (sub - 1) & sup;
} while(sub != sup); //处理完0之后，会有-1&sup=sup

枚举{0,1,…,n-1}的所有容量为k的子集

int comb = (1 << k) - 1;
while (comb < 1 << n) {
    //处理组合
    int x = comb & -comb, y = comb + x;
    comb = ((comb & ~y) / x >> 1) | y;
}

从(1«k)-1开始，求出其后的集合的方法。

1. 求出最低位的1开始的连续的1区间(0101110->0001110)
2. 将这一区间全部变成0，并将区间左侧的那个0变成1(0101110->0110000)
3. 将第一步的区间右移，直到剩下的1的个数减少了1个(0001110->0000011)
4. 将第二步和第三步的结果按位或(0110000|0000011=0110011)

x=comb&-comb 就是最低位的1独立出来后的值。-comb对应(~comb)+1。 y=comb+x 将最低位从1开始，连续的1都置零，区间左侧的那个0变成1。 z=comb&~y 得到最低位从1开始的连续区间。 z/x 将z不断右移，直到最低位为1，只要再向右移一位就是第三步的结果。

例如

comb = 0101110
   x = 0000010
   y = 0110000
   z = 0001110