给你一个足够大的薄饼,让你切n刀,最多能切出几片?或者换个说法,n条线最多可以把一个平面分成几份?
我们设定一个函数L(x),表示切x刀可以得到的切片数目。下面分别是x=0,x=1和x=2的样子。
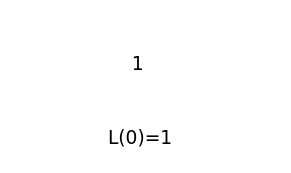
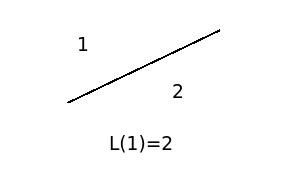
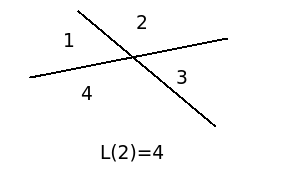
我们再切一刀,看看会发生什么?
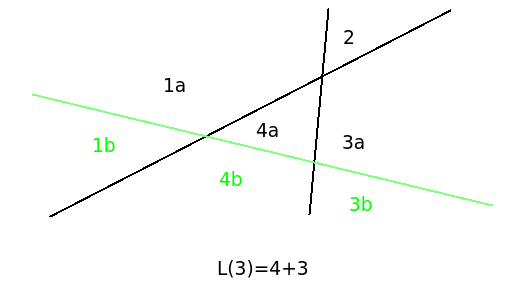
新的一条线把原来的部分1,4,3分成了1a,1b,4a,4b,3a,3b四个部分。显然,如果新的线跨过k个部分,那么它将把这k个部分都切成两份,也就是会多出k个部分。让新的线总是尽可能切割最多的已有部分,得到的切片数目就是最多的。那么,最多的数目到底是多少?
假设原来有k条线,那么这条新的直线最多可以和k条直线相交,可以想到的最好结果是,新的直线分割了k+1个切片,也就是说,如果原来有n-1条线,那么加入第n条线的时候,就会多出n个切片。由此,我们可以得到递推式。
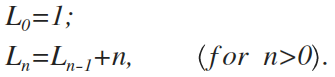
对于一些人来说,这样已经够了,但是我需要一个真正的答案,一个给出n就可以直接算出L(n)的函数。
把得到的递推式展开
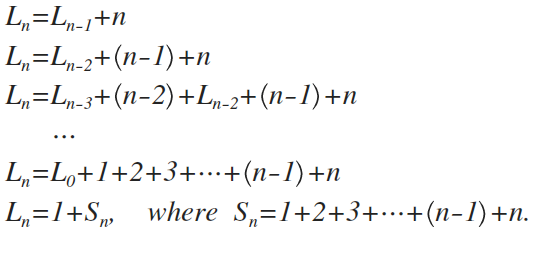
再进一步
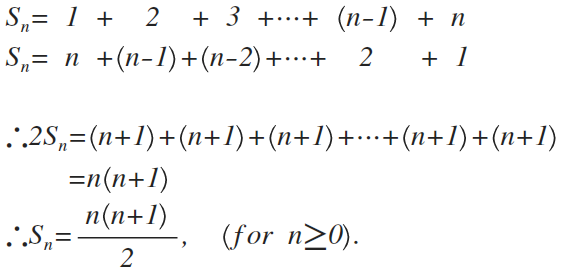
这就可以得到最终结果了
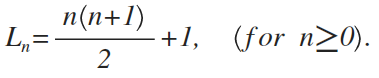
很多无良老师喜欢留下一些课后思考题以供娱乐学生,我也喜欢:)
如果给你的线不是直线,而是一个角(如下图)怎么办?
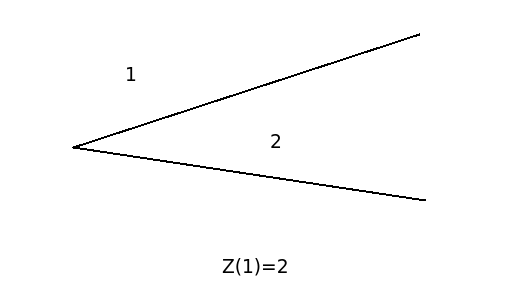
怎么办?
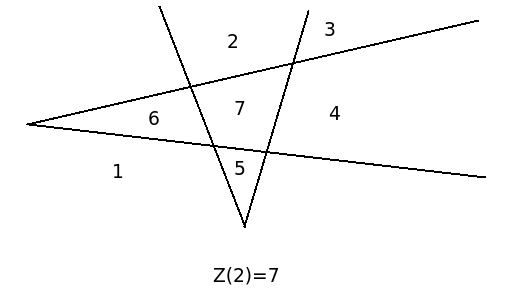
下面就是答案,其实把这个公式放在这里就是为了让那些只想得到最后结果直接不看过程的人生活过得“丰富”一些。
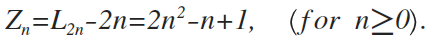
提示:只要让尖角离各种交点远一些就可以了。