kmp，字典树和AC自动机

13 March 2015

字符串匹配问题

给你一个字符串$s1$，$s1$是否包含子串$s2$举例来说，有一个字符串”BBC ABCDAB ABCDABCDABDE”，我想知道，里面是否包含另一个字符串”ABCDABD”？

最原始的做法是，先比较第一个字符，发现$s_1[0]=s_2[0]$；再比较第二个字符，发现$s_1[1]=s_2[1]$，再比较第三个字符，发现$s_1[2]=s_2[2]$； 等比较到第四个字符时，$s_1[3]$是空格，$s_2[3]=D$，匹配失败了，于是将$s2$右移，继续尝试匹配。

id: 0123456789...
s1: ABC ABCDAB ABCDABCDABDE
    |||X
s2: ABCDABD

右移后第一次尝试$s_1[1]=B\not= s_2[0]=A$，匹配失败，再次将$s2$右移。

id: 0123456789...
s1: ABC ABCDAB ABCDABCDABDE
     X
s2:  ABCDABD

再次右移发现还是不匹配，如此反复。右移4次之后，得到下面的结果，还是不能匹配，差了一个字符。

id: 0123456789...
s1: ABC ABCDAB ABCDABCDABDE
        ||||||X
s2:     ABCDABD

我们不断尝试匹配，如果匹配失败就将$s_2$右移，直到$s_2$的最后一个字符匹配成功，或者已经超出了$s_1$的长度范围从而匹配失败。

id: 0123456789...
s1: ABC ABCDAB ABCDABCDABDE
                   |||||||
s2:                ABCDABD

上述思想编程代码就是下面这个样子。算法复杂度很明显是$O(nm)$，其中$n$和$m$分别是$s_1$和$s_2$的长度。

 1 /*
 2  * does s2 is a substring of s1 ?
 3  * return NULL if not
 4  * return pointer which point to the first matching position of s1 if match
 5  */
 6 const char* matchStr(char const s1[], char const s2[]) {
 7     int offSet = 0, i, len1 = strlen(s1), len2 = strlen(s2);
 8     while (offSet + len2 <= len1) {
 9         for (i = 0; i + offSet < len1; i++) {
10             if (s1[offSet + i] != s2[i]) {
11                 offSet += 1;
12                 break;
13             }
14             if (i == len2 - 1) {
15                 return s1 + offSet;
16             }
17         }
18     }
19     return NULL;
20 }

kmp 算法

Knuth-Morris-Pratt算法（简称KMP)是由高德纳（Donald Ervin Knuth）和沃恩·普拉特在1974年构思，同年詹姆斯·H·莫里斯也独立地设计出该算法，最终由三人于1977年联合发表。这个算法的复杂度可以达到$O(m+n)$。

前面的方法将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把”搜索位置”移到已经比较过的位置，重比一遍。

首先，要了解两个概念：”前缀”和”后缀”。 “前缀”指除了最后一个字符以外，一个字符串的全部头部组合；”后缀”指除了第一个字符以外，一个字符串的全部尾部组合。

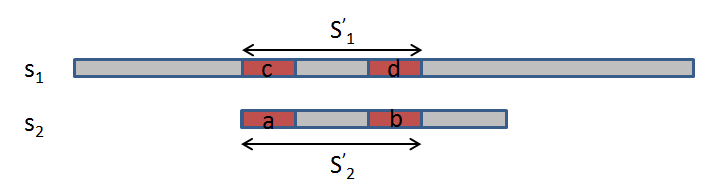
picture kmpp

上图中$s_2$已经匹配到了$s_2’$，但是紧跟着$s_2’$之后的那个字符和$s_1$对应位置的字符匹配失败了。$a$和$b$分别是$s_2’$的前缀和后缀，我们假设他们是相等的($a=b$)，并且是”前缀”和”后缀”的最长的共有部分。因为已经匹配到了$s_1’$，所以$s_1’=s_2’$，因此可以知道$d=b=c=a$，所以$a=d$，且$a$和$d$这是$s_2’$的前缀和$s_1’$的后缀的最长共有部分。当$s_2’$之后一个字符匹配失败时，我们可以直接将$s_2$右移到$a$和$d$对应的位置，而不是只向右移动一位。

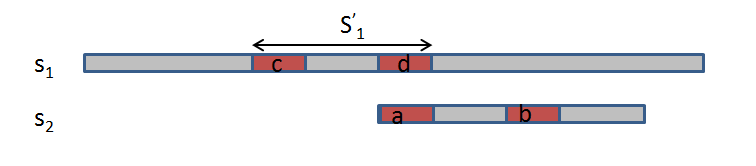
picture kmpp2

下面我们介绍使用动态规划方法计算$s_2$的前缀的最长相等前后缀，并存在部分匹配表$next$中。

$next[i]$的意思是在字符串$s_2[0..i]$中，最长公共前后缀的长度减一。也就是说，$s_2[0..next[i]]$就是$s_2[0..i]$的最长公共前后缀的内容。如果最长公共前后缀长度为$0$，我们约定对应$next$值为$-1$。

比如字符串$s_2=$”ABCDABD”，它的$next$数组如下。

s2   : A B C D A B D
next :-1-1-1-1 0 1-1

pucture kmpp3

假设右边箭头之前位置$next[0..i-1]$的值已经求出来了，$next[i-1]=j$，要求$next[i]$，怎么办呢？

因为$next[i-1]=j$，所以$s_2[0..j]=s_2[i-2-j..i-1]$；如果$s_2[j+1]=s_2[i]$，就可以认定$s_2[0..j+1]=s_2[i-2-j..i]$，所以$next[i]=j+1$；如果$s_2[j+1]\not=s_2[i]$，就让$j=next[j]$，重复上述过程；如果$j=-1$且$s_2[j+1]\not=s_2[i]$，那么$next[i]=-1$，表示没有相等前后缀。

 1 /*
 2  * return next array of string str[]
 3  */
 4 int * generateNext(const char str[]) {
 5     int i, j, len = strlen(str);
 6     int *next = (int*)malloc(len * sizeof(int));
 7     next[0] = j = -1;
 8     for (i = 1; i < len; i++) {
 9         next[i] = -1;
10         while (j != -1 && str[j + 1] != str[i]) {
11             j = next[j];
12         }
13         if (str[j + 1] == str[i]) {
14             j = next[i] = j + 1;
15         }
16     }
17     return next;
18 }
19 /*
20  * does s2 is a substring of s1 ?
21  * return NULL if not
22  * return pointer which point to the first matching position of s1 if match
23  */
24 char * kmpMatch(const char s1[], const char s2[]) {
25     int* next = generateNext(s2)， i = -1;
26     const char *p = s1;
27     while (*p != '\0' && s2[i + 1] != '\0') {
28         if (*p == s2[i + 1]) {
29             p++;
30             i++;
31         }
32         else {
33             if (i == -1) {
34                 p++;
35             }
36             else {
37                 i = next[i];
38             }
39         }
40     }
41     free(next);
42     if (s2[i + 1] == '\0') {
43         return p - i - 1;
44     }
45     return NULL;
46 }

如前面说的，有了$next$数组，做字符串匹配时，如果$s_2[i]$匹配成功，则继续向后匹配$s_2[i+1]$，如果匹配失败，则返回前面匹配$s_2[next[i]+1]$。

字典树

给你一个字符串集合$P$，问任意一个字符串$s$是否属于$P$。

前面讲过kmp算法，我们当然可以让$s$和$P$中所有元素比较，如果$\exists c \in P$使得$c=s$，我们就说$s$属于$P$，否则就说$s$不属于$P$。还有没有更有效率的算法呢？字典树（trie）就是专门处理这类问题的数据结构。

现在约定这一节我们使用的字符集是26个小写字母。

一个$P$的字典树是这样一个有根树$K$：

  1. $K$的每条边标一个字符
  2. 一个节点的任意两条边标着的字符不同，从根节点走到节点$v$经过的字符按经过顺序组成的字符串记为$L(v)$
  3. 对于任意$s\in P$，$\exists v\in V(K)$使得$L(v)=s$

比如，

则$P$对应的字典树是这个样子的

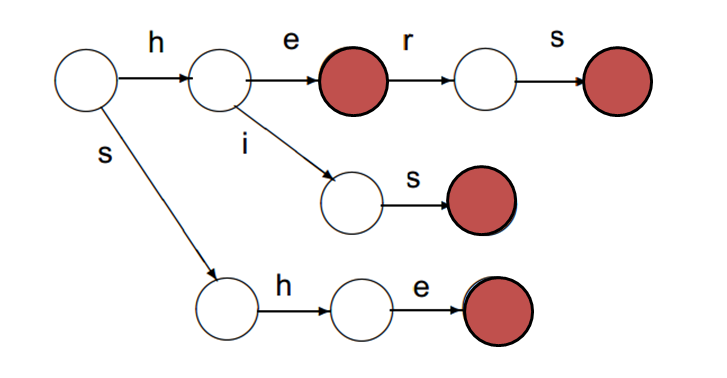
picture trie

上色的节点表示那些$L(v)\in P$的那些节点。要想知道$s$是否属于$P$，只需要从根节点开始，看看沿着$s$的字符标示的边向下走能不能最后走到一个上色的节点即可。

代码实现和二叉树类似，比较简单。如果嫌每个节点都开那么多指针太耗费空间的话，可以先把字符串都转化为二进制，这样字符集里就只有0和1了。当然，复杂度会稍微上升一些。

 1 #define MAXCHAR 26
 2 #define TRUE 1
 3 #define FALSE 0
 4 
 5 typedef struct NODE {
 6     int flag;
 7     struct NODE * childs[MAXCHAR];
 8 } Node;
 9 
10 Node * newNode() {
11     return (Node*)memset(malloc(sizeof(Node)), 0, sizeof(Node));
12 }
13 
14 Node *createTrie() {
15     return newNode();
16 }
17 
18 void destroyTrie(Node *T) {
19     int i;
20     for (i = 0; i < MAXCHAR; i++) {
21         if (T->childs[i]) {
22             destroyTrie(T->childs[i]);
23         }
24     }
25     free(T);
26 }
27 
28 void insertTrie(Node * const T, const char * const p) {
29     if (*p == '\0') {
30         T->flag++;
31     }
32     else {
33         if (T->childs[*p - 'a'] == NULL) {
34             T->childs[*p - 'a'] = newNode();
35         }
36         insertTrie(T->childs[*p - 'a'], p + 1);
37     }
38 }
39 
40 int isInTrie(Node *T, const char * const p) {
41     if (*p == '\0' && T->flag) {
42         return TRUE;
43     }
44     if (T->childs[*p - 'a']) {
45         return isInTrie(T->childs[*p - 'a'], p + 1);
46     }
47     return FALSE;
48 }

AC自动机

给出n个单词，再给出一段包含m个字符的文章，找出有多少个单词在文章里出现过。比如hers这篇只有4个字符的文章，出现了he、hers两个在P中的单词。

AC自动机算法分为3步：构造一棵Trie树，构造失败指针和模式匹配过程。

看过前面的KMP算法，AC自动机算法应该好理解了，就是用类似AC自动机的方法，寻找字典树上每个节点的$fail$值，思想也是和KMP类似的。$fail$值的意思是如果在当前节点找不到可以匹配的孩子节点，那么就转到$fali$指向的节点继续匹配。

$P$对应的自动机长得像这样，虚线表示的是$fail$值指向的位置。

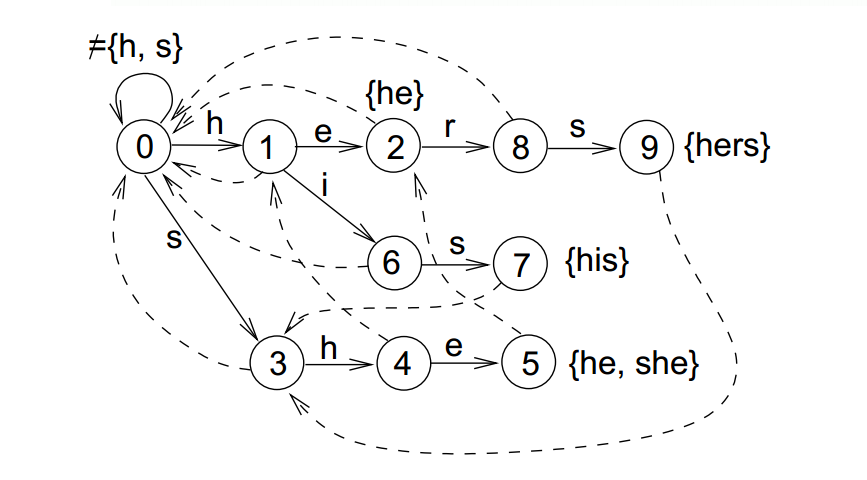
picture ac1

构造失败指针的过程概括起来就一句话：设这个节点上的字母为$C$，沿着他父亲的失败指针走，直到走到一个节点，他的儿子中也有字母为$C$的节点。然后把当前节点的失败指针指向那个字母也为$C$的儿子。如果一直走到了$root$都没找到，那就把失败指针指向$root$。可以用广度优先搜索的方式遍历整棵字典树，同时计算每个节点的$fail$值，这样可以保证遍历到某个点时，它的所有前缀对应的$fail$值已经被计算过。

 1 const int maxchar = 26;
 2 
 3 struct Node {
 4     Node *childs[maxchar];
 5     Node *fail;
 6     int count;
 7     Node() {
 8         count = 0;
 9         fail = NULL;
10         memset(childs, 0, sizeof childs);
11     }
12 };
13 
14 struct AC {
15 private:
16     Node *root;
17     void _insert(Node * const root, const char * const p) {
18         if (*p == '\0') {
19             root->count++;
20         }
21         else {
22             if (root->childs[*p - 'a'] == NULL) {
23                 root->childs[*p - 'a'] = new Node();
24             }
25             _insert(root->childs[*p - 'a'], p + 1);
26         }
27     }
28     void _destroy(Node *root) {
29         for (int i = 0; i < maxchar; i++) {
30             if (root->childs[i]) {
31                 _destroy(root->childs[i]);
32             }
33         }
34         delete root;
35     }
36 public:
37     AC() {
38         root = new Node();
39     }
40     ~AC() {
41         _destroy(root);
42     }
43 
44     /*
45      * insert a word
46      */
47     void insert(char *p) {
48         _insert(root, p);
49     }
50     void getFail() {
51         queue<Node *> que;
52         que.push(root);
53         root->fail = NULL;
54         while(!que.empty()) {
55             Node *e = que.front(); que.pop();
56             for (int i = 0; i < maxchar; i++) {
57                 Node *pre = e->fail;
58                 Node *cur = e->childs[i];
59                 if (cur) {
60                     que.push(cur);
61                     while (pre && !pre->childs[i]) {
62                         pre = pre->fail;
63                     }
64                     if (!pre) {
65                         cur->fail = root;
66                     }
67                     else {
68                         cur->fail = pre->childs[i];
69                     }
70                 }
71             }
72         }
73     }
74     int query(const char *p) {
75         Node *cur = root;
76         int ret = 0;
77         do {
78             while (cur != root && !cur->childs[*p - 'a']) {
79                 cur = cur->fail;
80             }
81             cur = cur->childs[*p - 'a'];
82             cur = cur ? cur : root;
83             Node *tmp = cur;
84             while (tmp != root) {
85                 ret += tmp->count;
86                 tmp = tmp->fail;
87             }
88         } while (*(p++));
89         return ret;
90     }
91 };
blog comments powered by Disqus